@TOC
一. 保凸运算
利用保凸运算可以从一个凸集构造出其他凸集。
1.1 交集
- 交集是保凸运算,这个交集可以扩展到无穷多个。
- 因此,常见的凸集:超平面,子空间,仿射集合对于交集运算也是封闭的。因此,多面体是半空间和超平面的交集,因此,也是一个凸集。
例1:半正定锥:
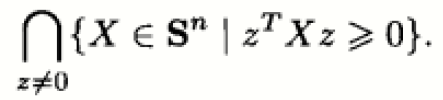 例2:傅里叶级数展开
例2:傅里叶级数展开
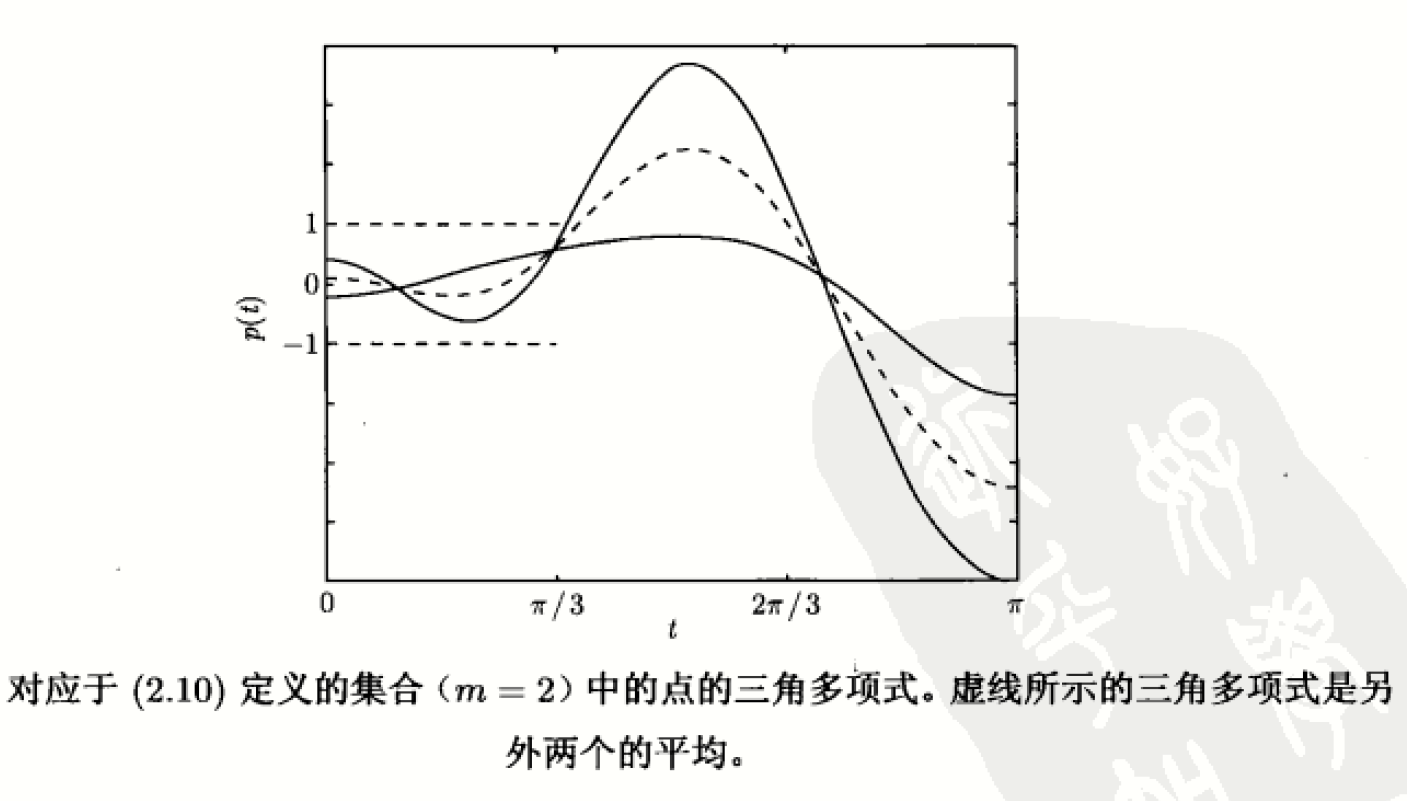
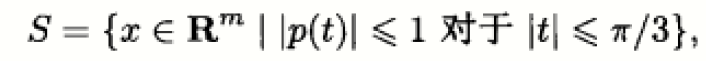 对于任意固定的t,它是一个n-1维超平面,其交集运算保凸,因此这个集合是凸集。其图像:
对于任意固定的t,它是一个n-1维超平面,其交集运算保凸,因此这个集合是凸集。其图像:
1.2 放缩,平移,仿射函数的逆函数
对于放射函数而言,即函数具有f(x)=Ax+b的形式,那么,函数:
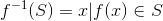 也是凸集。
仿射函数的两个例子就是放缩和平移。此时A为单位矩阵的实数倍,或者a是某个平移的冲击响应。
两个集合的直和和笛卡儿积是两个仿射函数的例子(数量值函数和向量值函数):
也是凸集。
仿射函数的两个例子就是放缩和平移。此时A为单位矩阵的实数倍,或者a是某个平移的冲击响应。
两个集合的直和和笛卡儿积是两个仿射函数的例子(数量值函数和向量值函数):
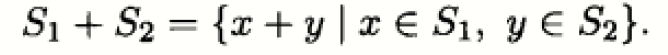
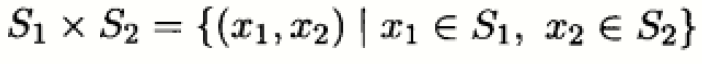
1.3 透视函数
透视函数是一个典型的线性分式函数,它也是保凸运算。

1.4 线性分式函数
二. 凸函数
2.1 定义
- 定义域是凸集
- convex定义为从
首先,事件A 产生的信息取决于事件A 发生的概率。因此信息应该是概率的函数。
假设事件A 以概率p 发生,那么如果事件A 发生了,它带来的信息是I(p),如果事件A 没有发生,它带来的信息是I(1-p)。那么在我们不知道事件A 发生没发生之前,它蕴含的信息就应该是
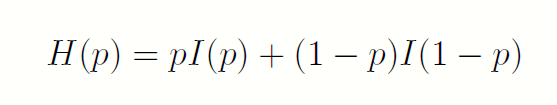 这就是平均信息量的来由。
这就是平均信息量的来由。
1.1.2 I(p)的确定
那么I(p)应当如何确定?,从描述的概念来说,它应该满足这些概念:
- 1.I(p)>=0, 即非负性,信息不应该是负的。
- 2.I(pq)=I(p)+I(q),即独立事件相加性,两个独立事件所给出的信息应该是相加的。
可以证明,满足这三个条件的函数I 只可能是以下形式:
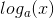 为了确定常量a,需要将单位1的信息量标准化:
为了确定常量a,需要将单位1的信息量标准化: - 3.I(1/2) = 1,标准化,假设概率为1/2 的事件给我们的信息是1
由此,一个取{0; 1} 的二进制随机变量X,如果取0(或者1)的概率为p,那么这个随机变量包含的平均信息就是:
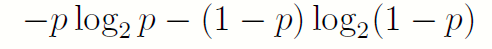
1.1.3 熵的引入
由此,当一个m 进制的随机变量Y ,取值为{1; 2; … ;m},取k 的概率为pk 时,它包含的信息量就是:
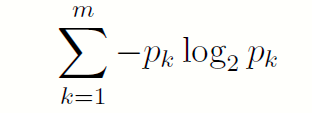 且:
且:
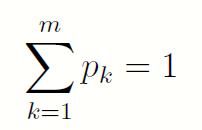
1.2 熵的定义
信息虽然是个相当宽泛的概念,很难用一个简单的定义将其完全准确地把握,然而,对于任何一个概率分布,可以定义一个称为熵(entropy)的量,它具有许多特性符合度量信息的直观要求。信息熵是描述信源统计的一个客观物理量。它首先是1948 年香农给出的,后来Feinstein 等人又从数学上严格的证明了当信息满足对概率递降性和可加性条件下,上述信息熵的表达形式是唯一的。对于一个在$\Chi$上定义的离散随机变量,其熵有两种定义:
1.2.1概率形式的定义
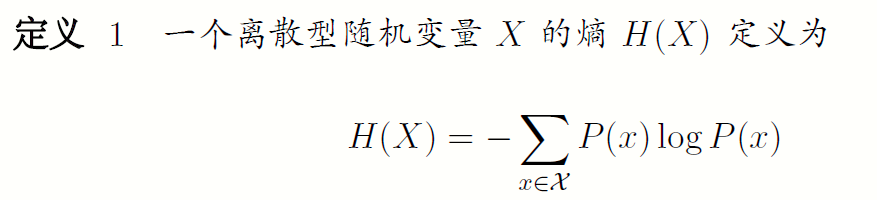 有时也将上面的量记为H(P),其中对数log 所用的底是2,熵的单位用比特表示。例如,抛掷均匀硬币这一事件的熵为1 比特。由于当x趋于0时,xlogx趋于0,今后我们约定0log0=0,因此,加上零概率的项不改变熵的值。
信息熵的单位与公式中的对数取底有关。如果使用底为b 的对数,则相应的熵记为$H_b(X)$。通信与信息中最常用的是以2为底,这时单位为比特(bit);理论推导中用以e 为底较方便,这时单位为奈特(Nat);工程上用以10 为底较方便,这时单位为笛特(Det)。如无特别说明,一般选取对数底为2,因而熵的量纲一般情况下为比特。注意,熵实际上是随机变量X 的分布的泛函数,并不依赖于X 的实际取值,而仅依赖于其概率分布。
有时也将上面的量记为H(P),其中对数log 所用的底是2,熵的单位用比特表示。例如,抛掷均匀硬币这一事件的熵为1 比特。由于当x趋于0时,xlogx趋于0,今后我们约定0log0=0,因此,加上零概率的项不改变熵的值。
信息熵的单位与公式中的对数取底有关。如果使用底为b 的对数,则相应的熵记为$H_b(X)$。通信与信息中最常用的是以2为底,这时单位为比特(bit);理论推导中用以e 为底较方便,这时单位为奈特(Nat);工程上用以10 为底较方便,这时单位为笛特(Det)。如无特别说明,一般选取对数底为2,因而熵的量纲一般情况下为比特。注意,熵实际上是随机变量X 的分布的泛函数,并不依赖于X 的实际取值,而仅依赖于其概率分布。1.2.2 数字特征形式的定义
将1.2.1中的熵定义为如下形式:
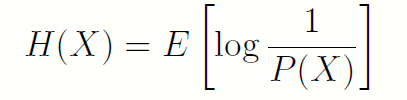 这是一个怪异的均值引用,其随机变量的函数就是该随机变量下的概率本身。
这是一个怪异的均值引用,其随机变量的函数就是该随机变量下的概率本身。
二. 熵的基本性质
- H(X)>=0. 证明:由定义即可验证。
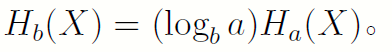 证明:由对数中的换底公式可以直接证明。
这告诉我们熵的定义中可以改变定义中对数的底。从I(p)的构造中我们就可以得知,单位信息量就是人为定义的,只要乘以适当的常数因子即可换底。
证明:由对数中的换底公式可以直接证明。
这告诉我们熵的定义中可以改变定义中对数的底。从I(p)的构造中我们就可以得知,单位信息量就是人为定义的,只要乘以适当的常数因子即可换底。- 以2为底的熵定义中的熵在数值熵等于为确定变量X所需的二元问题数的最小期望值。
- 当X均匀分布时,熵最大。
一个例子:0-1分布的X,其熵:
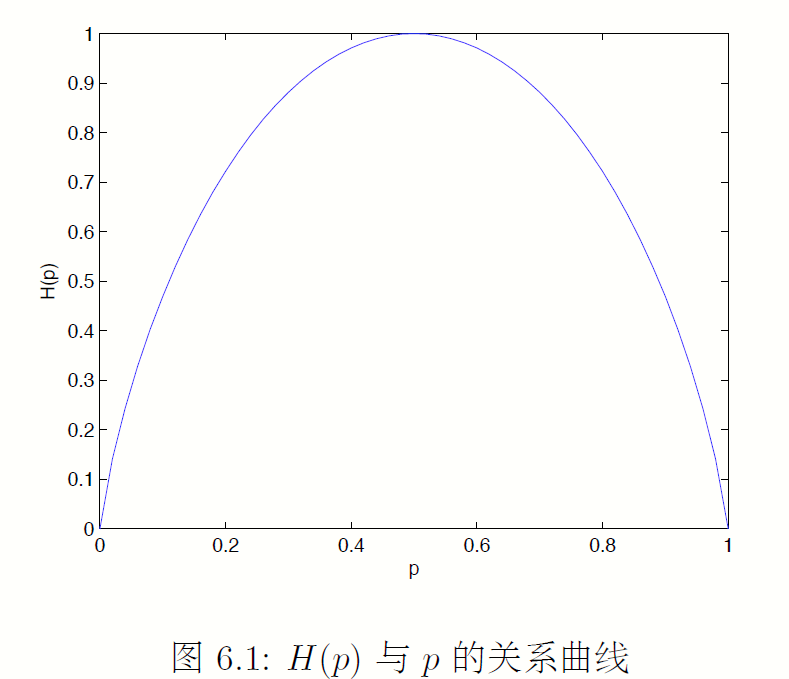
三. 联合熵和条件熵
3.1 联合熵
我们已经定义了一个随机变量的熵。下面我们把这个定义推广到一对随机变量。一对随机变量的上的定义没有任何新的元素在其中,因为(X; Y ) 可以被看成是一个随机变量,只不过它取矢量值。
- 若(X; Y) 的联合概率分布为P(x;y),联合熵H(X; Y) 的定义为:
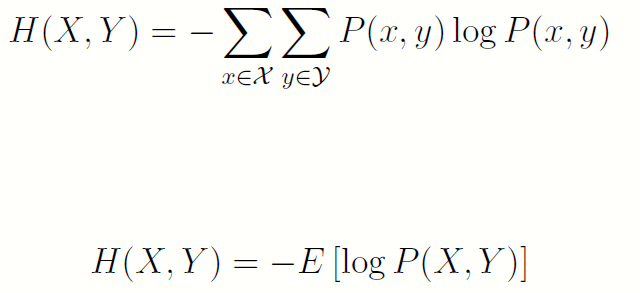 也就是说,可以将X,Y的变化(有限维矩阵)展成一个向量来理解,把其看成一元随机变量的熵。
也就是说,可以将X,Y的变化(有限维矩阵)展成一个向量来理解,把其看成一元随机变量的熵。
3.2 条件熵
下面我们定义给定一个随机变量,另一个随机变量的条件熵:
- 若(X; Y) 的联合概率分布为P(x;y),条件熵H(Y|X) 定义为:
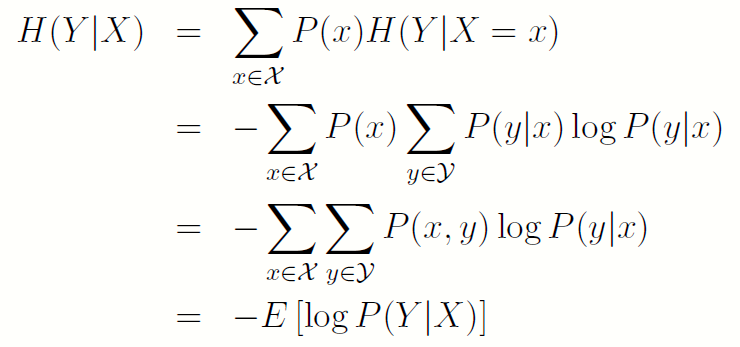 条件熵的定义是联合密度下条件概率的数学期望,切勿搞混!!
条件熵的定义是联合密度下条件概率的数学期望,切勿搞混!!
四. 条件熵的相关定理
4.1 链式法则
联合熵与条件熵的定义是恰当的,因为它们满足下面的定理:即两个随机变量X; Y 的不确定度等于X 的不确定度再加上已知X 后, Y 的不确定度。这也称为链式法则:
- H(X,Y)=H(X)+H(Y|X)
证明:
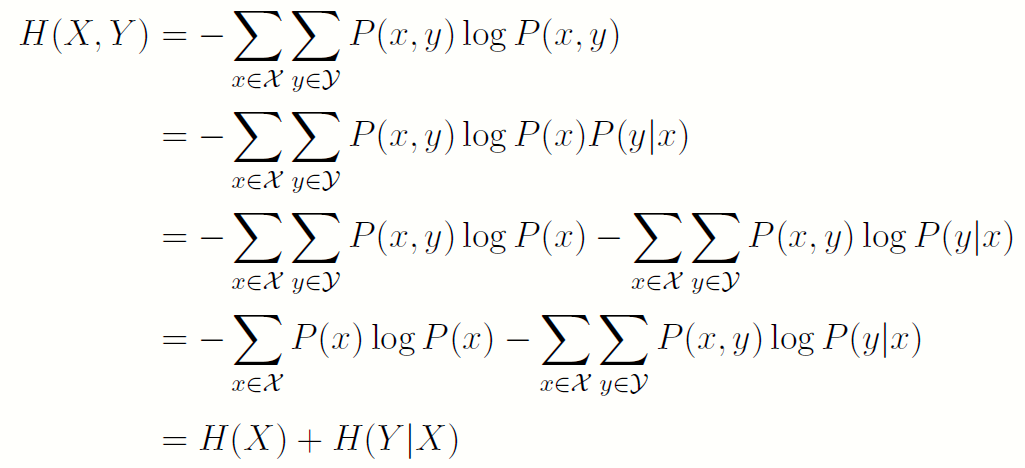 或者根据条件概率的定义,将其取对数之后都按分布P(x,y)取均值即可。
或者根据条件概率的定义,将其取对数之后都按分布P(x,y)取均值即可。
4.2 n个随机变量的链式法则
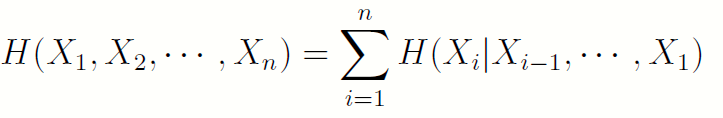 证明:多次使用链式法则的推论即可。
证明:多次使用链式法则的推论即可。4.3 链式法则的相关推论
-
H(X,Y)=H(X)+H(Y X)=H(Y)+H(X Y) - H(Y)-H(Y|X)=H(X)-H(X|Y)
4.4 知识降低熵
- H(X)>=H(X|Y)
从直观上讲,此定理说明知道另一随机变量Y 的信息只会降低X 的不确定度。注意,这仅对平均意义成立。具体来说, H(X|Y=y)可能比H(X)大或者小,或者两者相等。
4.5 独立时熵最大
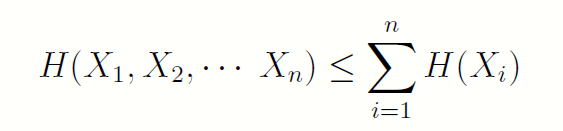 当且仅当各个Xi独立时,等号成立。
当且仅当各个Xi独立时,等号成立。
| 课时数 | 内容 | 作业 | 答案 | 主要要求 |
|---|---|---|---|---|
| 1 | 导引,基本化学概念 | 初中复习课1 | ||
| 2 | 物质的基本性质(一) | 初中复习课2 | ||
| 3 | 物质的基本性质(二) | 初中复习课3 | ||
| 4 | 物质的基本性质(三) | 初中复习课4 | ||
| 5 | 物质的量 | 概念,原理 | ||
| 6 | 物质的量的应用,习题课1 | 计算,应用 |