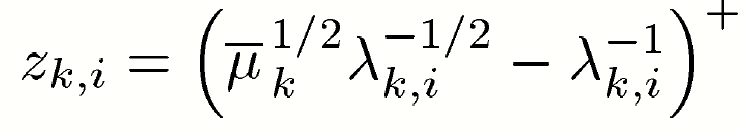@TOC 本文讲义下载地址：多载波MIMO信道下的波束成形设计
1. Multicarrier Communication & OFDM
见Multicarrier Communication & OFDM
2. Majority Theory & Schur Convex Analysis
2.1 向量的受控关系
2.1.1 受控关系的定义
Definition1: (x↓和x↑) x∈R^n,将x=(x_1, x_2…x_n)的各个分量排成递减和递增后，记作:
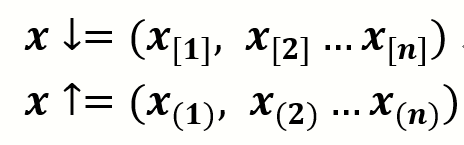
Definition2(受控关系): x,y∈R^n, e_1, e_2…e_n 为R^n上的单位向量，则：
(1). 若∃k=1…n-1,
称x被y控制，记作x≺y。特别的，若x不是y的重排，称x被y严格控制，记作x≺≺y。
注意:不同于x≤y, x≺y中x,y的分量顺序无关紧要，只与分量的大小有关。
2.1.2 受控关系举例
Eg1: R是一个n*n厄米矩阵，其对角元素构成向量d，其特征值构成向量c,则d≺c。
Eg2: x为任意n维向量，x1为x的均值向量，则x1≺x。
2.2 Schur凸函数和凹函数
Definition3(Schur-convex): f:R^n→R满足：
∀x，y∈R^n x≺y→f(x)≤f(y) 称f是Schur凸函数，若：
∀x，y∈R^n x≺y→f(x)≥f(y) 称f是Schur凹函数。
3. Signal Model
3.1 Carrier-noncooperative approach - Channel
We consider a communication system with 𝑛_𝑇 transmit and 𝑛_𝑅 receive dimensions. To deal easily with the frequency-selectivity of the channel, we take a multicarrier approach without loss of optimality:
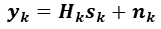
3.2 Carrier-noncooperative approach - Sender
The transmitted vector at the k-th carrier after linear precoding can be described:
3.3 Carrier-noncooperative approach - Receiver
The received vector at the k-th carrier after the equalizer is:
3.4 Comprehension
3.5 Carrier-cooperative approach
4. Optimality of Receive Matrix of the Channel-diagonalizing Structure
4.1 Instruction
In general, it is a complicated nonconvex problem, but for some specific design criteria, the original complicated problem is greatly simplified. Because the channel turns out to be diagonalized by the transmit-receive processing, which allows a scalarization of the problem.
4.1.1 Optimal criteria
- the minimization of the sum of the MSEs of all channel spatial substreams
- the minimization of the determinant of the MSE matrix
- the maximization of the mutual information
- the minimization of the average/maximum BER
- the maximization of the minimum SINR
- etc…
4.1.2 Optimal Functions:
we consider that the design is based on the minimization of some arbitrary objective function of the MSEs of all channel substreams:
𝑓_0 is an indicator of how well the system performs. Objective function 𝑓_0 must be increasing in each one of its arguments.4.2 MSE Optimization
4.3 BER/ Optimization
many objective functions are naturally expressed as functions of the SINR of each substream. The SINR at the k-th carrier and the i-th spatial substream is:
Maximizing the SINR is clearly equivalent to minimizing the MSE.
The performance of a digital communication system is ultimately given by the fraction of bits in error or bit error rate (BER):
Where k is the number of bits per symbol, and M is the constellation size.
It can be proved that the BER and the corresponding Chernoff upper bound are convex decreasing functions of the SINR and convex increasing functions of the MSE.
4.4 Lemmas of In/Decreasing
4.4.1 BER-SINR
- Lemma1: BER is convex decreasing functions of the SINR.
4.4.2 Chernoff upper bound-SINR
- Lemma2: Chernoff upper bound is convex decreasing functions of the SINR.
4.4.3 BER-MSE
- Lemma3: BER is convex increasing functions of the MSE.
To prove that the BER is convex increasing in the MSE, it suffices to show that the first and second derivatives are both positive :
where the zeros are
It is remarkable that for 𝛽=1, both zeros coincide, which means that the BER function is convex for the whole range of MSE values. Otherwise, BER is convex increasing of the MSE only when
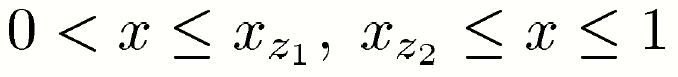
4.4.4 Chernoff upper bound BER- MSE
- Lemma4: Chernoff upper bound BER is convex increasing functions of the MSE.
To prove that the Chernoff upper bound of BER is convex increasing in the MSE, it suffices to show that the first and second derivatives are both positive :
BER is convex increasing of the MSE only when
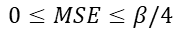
4.4.5 Conclusion
Lemma5: The exact BER function and the Chernoff upper bound are indeed convex in the MSE for a BER. Lemma6: Wiener filter has been obtained as the optimum linear receiver in the sense that it minimizes each of the MSEs, maximizes each of the SINRs, and minimizes each of the BERs
Proof: From Lemma1-4, lemma5,6 is obvious.
5. Optimality of Transmit Matrix of the Channel-diagonalizing Structure
5.1 Question described
5.2 Lemmas for Optimal Matrix
5.2.1 Rank Lemma
5.2.2 Lemma for the exact Matrix
5.3 Optimal Expect Value
5.4 Optimal MSE
5.5 Optimal SINR
5.6 Design Suggestion via SINR
5.7 Schur-convex case
Lemma3-5 are the results of a Schur-concave 𝑓_0
5.8 Conclusion & Multicarrier case
Conclusion of a single carrier:
- For Schur-concave functions, the specific power distribution among the established substreams will depend on the particular objective function 𝑓_0. Interestingly.
- For Schur-convex functions, the power distribution is independent of the specific choice of 𝑓_0 since both the MSE expression and the rotation matrix to make the diagonal elements of the MSE matrix equal are independent of 𝑓_0
Here question comes with a multicarrier case:
6. Joint TX-RX Beamforming Design
6.1 Optimal Criteria
Now the Optimal criteria:
- the minimization of the sum of the MSEs of all channel spatial substreams
- the minimization of the determinant of the MSE matrix
- the maximization of the mutual information
- the minimization of the average/maximum BER
- the maximization of the minimum SINR
is specified in practical.
6.2 ARITH-MSE
The minimization of the (weighted) arithmetic mean of the MSEs (ARITH-MSE) :
The objective function is
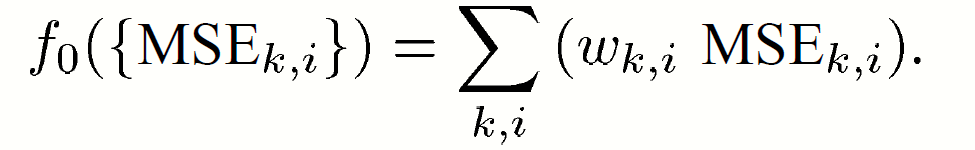Lemma1: The function is minimized when the weights are in increasing order , and it is then a Schur-concave function.
The problem in convex form (the objective is convex and the constraints linear):
the solution
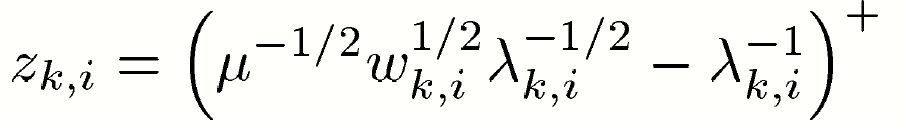the solution has a nice water-filling interpretation.
6.3 GEOM-MSE
the minimization of the weighted geometric mean of the MSEs (GEOM-MSE) :
The objective function is
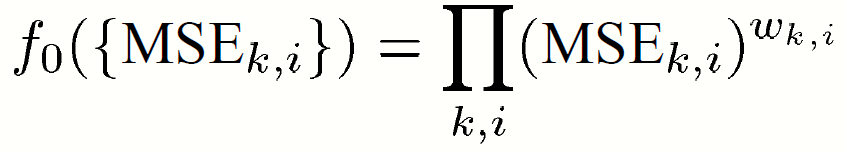Lemma2: The function is minimized when the weights are in increasing order , and it is then a Schur-concave function on each carrier k.
The problem in convex form (the objective is convex and the constraints linear):
the solution
6.4 MAX-MSE
minimize the maximum of the MSEs (MAX-MSE) :
The objective function is
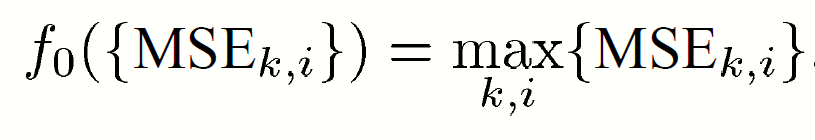Lemma3: The function is a Schur-convex function.
The problem in convex form (the objective is linear and the constraints convex):
the solution
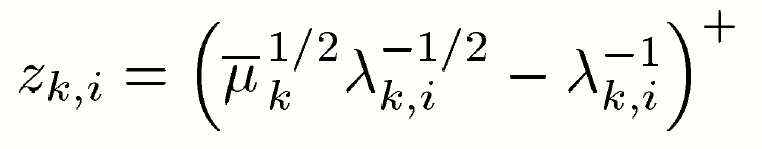
6.5 ARITH-SINR
minimized for the maximization of the (weighted) arithmetic mean of the SINRs (ARITH-SINR) :
The objective function is
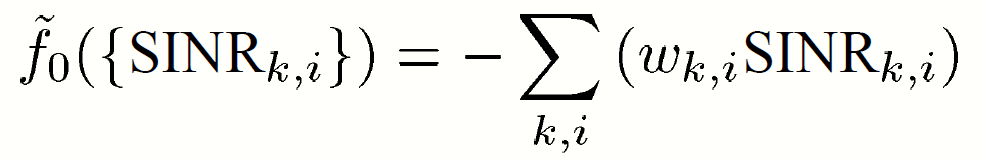It can be expressed as a function of MSEs:
Lemma4: The function is minimized when the weights are in increasing order , and it is then a Schur-concave function.
The problem in convex form (the objective is linear and the constraints convex):
the solution is to allocate all the available power to the substream with maximum weighted gain, which has extremely poor spectral efficiency.
6.6 GEOM-SINR
minimized for the maximization of the (weighted) geometric mean of the SINRs (GEOM-SINR) :
The objective function is
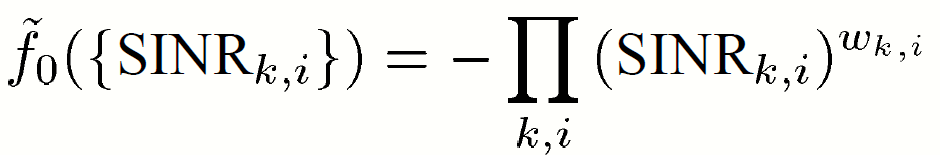It can be expressed as a function of MSEs:
Lemma5: The function is minimized when the weights are in increasing order , and it is then a Schur-concave function.
The problem in convex form (the objective is linear and the constraints convex):
the solution is
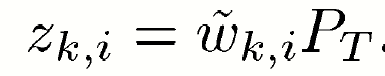
6.7 HARM-SINR
maximization of the harmonic mean of the SINRs (HARM-SINR) :
The objective function is
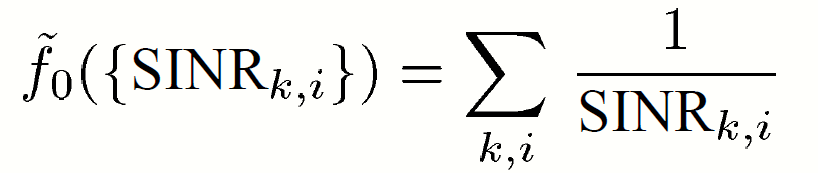It can be expressed as a function of MSEs:
Lemma6: The function is a Schur-convex function.
The problem in convex form (the objective is linear and the constraints convex):
the solution is
